
©2025, technoventure, inc.
ϕ Predefined Data Types
One of the weakest areas of the C Programming Language is its atomic typing system. Its basic integer type (int) is sized to match the target host's Word size. Typically this is the size of the host's integer registers (in bits or bytes). While providing a stack alignable data size is good in itself, not having integer types with known sizes robs the programmer of precise control of the data sizes when they are needed. An effective programmer will need to know exactly how many bits can be packed into a data structure and you really don't have that in C. Furthermore, in the post ASCII world of Unicode, type “char” has become a misnomer while being inexorably tied to the size of a byte. Ironically, it is the only integer size that is known for sure, but its name should imply that its size is appropriate for holding a Unicode character (the standard for today's text representation), which it is not.
Another incoherency in C is more subtle, but becomes more obvious when you think about it. One of the most basic aspects of any typing system is the notion of a Type Class. This refers to the rules that govern the behavior of all of the specific types belonging to the Type Class. (Note: Use of the key word “class” to specify a special kind of Type in object-oriented programming languages such as C++, C# and Java is another unfortunate misnomer that is the source of more confusion. It is an entirely different animal and we don't even need such a key word in ϕPPL any way.) The metric that distinguishes every Type within a Type Class is its Size. That is the number of bits or bytes that make it up. This should imply that every Type Class's definition contains one or more arrays of bits whose count is different for every specific type within the type class. This concept is backed up with syntax in ϕ and applies to both ϕPPL and ϕAsm.
ϕ Type Classes and Names
It took me a long time to unravel and rectify
the backwards syntax of C to create something that makes a lot
more sense. C uses the key words “unsigned”
and “signed” as though they
were adjectives to modify a size such as “int” or “float”
that acts like a noun. In ϕ we reverse these concepts. Key
words like “unsigned”, “signed” and “float” should instead be
thought of as nouns since they specify type classes that types
belong to. Size is then used as an adjective to specify the
specific type within its type class. Single word type names
are assigned to each of the predefined types without resorting
to additional key words such as “long
long int”.
Most of the general-purpsoe predefined types supported in ϕ belong to five type classes. These are “usg” (unsigned), “sgn” (signed), “num” (nullable unsigned integer), “int” (nullable signed integer) and “flt” (float). Each specific type within its type class is given a two-character name. The first character represents the type class. These are ‘u’ for usg, ‘s’ for sgn, ‘n’ for num, ‘i’ for int and ‘f’ for flt. The second character represents its magnitude which is a multiple of its smallest size. These naming rules are only used for types that belong to type classes. ϕ's predefined data types will be individually discussed in the sections that follow. Some of the predefined types do not belong to any type class and can be thought of as belonging to their own implied type classes.
ϕ Type Class Magnitudes
Single character magnitude designators are taken from English words that imply a numerical multiplier. The only exception is the first one which represents the most basic size of the type class. This is either “Byte” for integers or “Brief” for floating point. They share the single letter designation ‘b’. A Byte is the smallest unit of memory that is addressable and is an 8-bit value. Integer types are composed of a multiple of bytes. A Brief is the smallest of the IEEE754 floating point formats and is two bytes. Every floating point type has twice the size of its integer counterpart (i.e. shares the same magnitude). This is why we use magnitudes instead of sizes for naming the basic types. We will discuss each type class in more detail later on.
In ϕ we have two magnitude series. These are the ① Storage Magnitudes and the ② Working Magnitudes. The Storage Magnitudes are the linear series of eight: 1, 2, 3, 4, 5, 6, 7 and 8. This series defines the predefined magnitudes of the five general-purpose numerical type classes. The magnitudes larger than the base magnitude are all taken from commonly used words that imply their number. They are 1 for Byte/Brief, 2 for Double, 3 for Triple, 4 for Quadruple, 5 for Pentuple, 6 for Hexuple, 7 for Septuple and 8 for Octuple. The Working Magnitudes are the subset of the Storage Magnitudes in the exponential series 1, 2, 4 and 8. These should be familiar to experienced programmers because they are the ones that are alignable on their natural boundaries. They can be stored in arrays without being broken up into pieces when they are accessed. These single letter magnitude designators are tabulated below:
| Meaning | Byt/Brf | Dbl | Tpl | Quad | Pent | Hex | Sept | Oct |
|---|---|---|---|---|---|---|---|---|
| Designator | b | d | t | q | p | h | s | o |
| Magnitude | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 |
The two-letter type names are formed from the type class letter which comes first and then the letter that represents magnitude. These are the general-purpose numerical data types that are of known size. In other words, their use guarantees the number of bits and bytes that make them up. These names are tabulated below:
| Class↓/Mag→ | Byt/Brf | Dbl | Tpl | Quad | Pent | Hex | Sept | Oct |
|---|---|---|---|---|---|---|---|---|
| usg | ub | ud | ut | uq | up | uh | us | uo |
| sgn | sb | sd | st | sq | sp | sh | ss | so |
| num | nb | nd | nt | nq | np | nh | ns | no |
| int | ib | id | it | iq | ip | ih | is | io |
| flt | fs | fd | ft | fq | fp | fh | fs | fo |
The full names for the above data types are called “Unsigned Byte” for ub, “Signed Byte” for sb, “Number Byte” for nb, “Integer Byte” for ib, “Float Brief” for fb, “Signed Double Byte” for sd, “Unsigned Triple Byte” for ut and so forth. I frequently use these type names even in C and they save a lot of source code space. A basic feature of ϕ is that you can see a lot of meaning in a small amount of text. This is the benefit of a more compact syntax augmented with Unicode where it makes sense to do so.
Alignment and
Padding
Main stream programming languages don't
support most of the data types discussed above. For some of
them, presumably it is because they are not alignable on their
natural boundaries. But this is short-sighted. A conscientious
programmer will carefully select each data type to cover the
range of values that are to be expected in the application.
Values naturally occur in ranges that follow an exponential
series. When you make a data type one byte longer, you are
exponentially increasing its range of values. When you double
the number of bytes, you increase its range much faster than
that. It is two-orders of exponential. So it makes more sense
to provide a linear series rather than an exponential series
of sizes just to satisfy the needs. After all, our computers
are byte-addressable.
There are two factors that impact the
efficacy of a data type's alignability. First is how easily
elements are accessed in arrays. When element sizes correspond
to an exponential series, you can use shifts instead of
multiplies to calculate an array element's location in memory
given the array's base address and element's index. The second
factor concerns keeping a machine stack aligned. In real world
applications, different values are frequently kept paired
together in records. In such cases, it is more important that
the record is alignable than the individual members within the
record. It is my belief that a programming language should
leave such decisions up to a responsible programmer rather
than having an alignment convention enforcing unwanted padding
to ensure alignment. ϕ places memory usage efficiency at a
higher priority than raw performance. Generally-speaking,
keeping the machine stack word aligned is one of the few cases
where data alignment is enforced. Machine stacks are, by their
nature, temporary holding areas for data and so enforcement of
their alignment is justified.
ϕ's Most Fundamental Type bo
Type bo is the most fundamental of all types in ϕ. It represents the bit and all higher types are derived from it. All of the predefined data types are already defined before you even type the first character of code into your program. Even though you don't have to write these definitions yourself, it is still useful to know what they look like so that you can define your own. This topic will be covered in more depth in the section on ϕPPL.
ϕ Type Class usg (Unsigned)
Eight Unsigned Integer data types of known sizes belong to the type class usg. Each one is constructed as a multiple of the smallest size which is one byte. They can have values of 0 ∼ 256Mag−1. Type ub can take on a value of 0 to 255. Type ud can take on a value of 0 to 65535 and so on. Experienced programmers will already be familiar with unsigned integers. The only things we have that are new are the non Working Types that do not align on their natural boundaries. Global datums are not padded for alignment in executable programs. You can't align non-alignable types anyway. This contributes to ϕ programs being more compact than those of main stream systems.
ϕ Type Class sgn (Signed)
Eight signed integer data types of known sizes belong to the type class sgn. Each one is constructed as a multiple of the smallest size which is one byte and can take on a value from −2Mag×8−1 ∼ +2Mag×8−1−1. So type sb can have a value of −128 to +127. Type sd can take on a value of −32768 to +32767 and so on. New to experienced programmers will be the non-alignable types ut, up, uh and us. What I wrote about alignment and padding in the previous section on unsigned integer types also applies to the signed integer data types. Values of this class are encoded as Two's Complement Numbers which have interesting behavior making them similar to unsigned integers. When values are added they wrap around as do unsigned numbers. Incrementing a sb with a value of +127 will wrap around to the value of −128. Decrementing a value of −128 will wrap around to +127.
ϕ Type Class num (Number)
Eight Nullable Unsigned Integer data
types of known sizes belong to the type class num. They are identical with those
of type class usg except for
one thing. The highest value has the special meaning of ⊙ (256Mag−1). This is the
symbol used to represent Nulls in ϕ. Valid values are 0 ∼ 256Mag−2.
Type nb can take on a value
of 0 to 254 or ⊙. Type nd can
take on a value of 0 to 65534 or ⊙ and so on.
ϕ Type Class int (Integer)
Eight Nullable Signed Integer data
types of known sizes belong to the type class int. Each one is constructed as a
multiple of the smallest size which is one byte and can take
on a value from −2Mag×8−1−2 ∼ +2Mag×8−1−1.
So type ib can have a value
of −127 to +127 or ⊙. Type id
can take on a value of −32767 to +32767 or ⊙ and so on. An
interesting feature of this type class is that every value has
a valid value with the opposite sign. That is not true with
type class sgn. If you negate
its most negative value it will overflow because the
representation has no equivalent positive value. By contrast,
negating any value of type class int
will not cause overflow. And if you negate a Null value you
will end up with a Null value which is as it should be.
ϕ Type Class flt (Float)
The binary formats and behavior of ϕ's type class flt data types follow the IEEE754 floating point standard. There are eight of them and they are all of known sizes. Since the standard only defines what ϕ calls the types with Working Magnitudes, the other four non-alignable Storage Types were derived by interpolating between them. These data types all have one bit for storing the sign. The other two fields are the Exponent and the Significand. The latter is somewhat equivalent to the Mantissa of the so-called Scientific Notation. The sizes in bits of all of the fields for all eight types are tabulated below:
| Bit Field↓/Type→ | fb | fd | ft | fq | fp | fh | fs | fo |
|---|---|---|---|---|---|---|---|---|
| Sign | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 |
| Exponent | 5 | 8 | 10 | 11 | 12 | 13 | 14 | 15 |
| Significand | 10 | 23 | 37 | 52 | 67 | 82 | 97 | 112 |
| Total | 16 | 32 | 48 | 64 | 80 | 96 | 112 | 128 |
ϕ Word-Aligned Integer Types
ϕ has four integer data types with the size of the host processor's word. Because of this, the programmer does not know from the context of the source code how large a word is. He/she must glean that information knowing how the compiler will interpret them and that may be influenced by the options that are configured for the compiler. Given a full set of data types that come with the ϕ SWDev tools, I rarely need such a data type. Perhaps they will find the most use when writing system code for ϕOS because it must deal more directly with machine stacks. But they are available in cases where they might find use. You should be aware that writing code with these data types makes your code somewhat non-portable because the ranges of values that are representable by different sizes vary from one system to another. Type uw is equivalent to C's “unsigned int” and type sw is equivalent to C's “signed int”. C has no equivalent or nw or iw. Recall that “signed” is assumed when missing within the context of C source code. You don't have to worry about this anomaly in ϕ. Note that there is no equivalent word-alignable float type.
ϕTime Types tim and tic
Time measurement systems used in computer software can be very complicated. There are 60 seconds in a minute, 60 minutes in an hour, 24 hours in a day and 365 plus an odd fraction close to 1/4 of a day in a year. Milliseconds and other fractional units are used to measure short passages of time. Factoring their various parts gives you a complicated mix of bases including 2, 3, 5 and something that is locked to the Earth's period of orbit around the sun. Measurement and processing of time in ϕ is extremely simple by comparison. Think of absolute time as a signed fixed-point binary number. The unit of ϕTime is the second and the fraction is 1/128 of a second. But you can treat 1/128 second as the unit. A 64-bit signed integer value containing these increments of time defines the type called tim and is used to record absolute dates and times in ϕ. The format is illustrated below:

Bits 0∼6 record the fraction of a second while bits 7∼63 record the second. It spans about 4.64 billion years which is about the age of the Earth and its star. But it is a signed number centered around midnight beginning January 1 in the year 1 BCE. There is no year 0 AD (or 0 BCE) in the Gregorian calender and it starts with the year 1 BCE. This makes the positive year numbers line up but the negative ones will be off by one. It is better to have to adjust the years you don't use every day than the ones you do. As a signed value, the span is divided into two halves of equal time. Negative values cover about 2 1/4 billion years in the past which includes most of the time life has existed on Earth. Positive values cover the same amount of time into the foreseeable future. This format is to be used by computers for recording dates and time of day and should never expire during its useful life as happened for Y2K. Our species will certainly be extinct well before this number overflows. Every ϕOS system maintains a system date/time using this format. As simple as this system is, there will be occasions when values need to be converted to and from other familiar representations. The complexities of those algorithms are well understood and are hidden in routines to serve the purpose.

ϕTime defines a second time format called tic illustrated above. This format corresponds to the low-order half of tim and can be treated as an unsigned 32-bit integer. It contains the fractional portion of a second along with 25 integer bits. Each increment in time (called a tic as in the ticking of a clock) represents the smallest unit of time that is resolved when processing in real time. There is nothing that can be scheduled into the past and this is why it represents an unsigned relative time into the future. It is used by ϕOS to schedule events. The time span gives you about one year and three weeks into future. A week or so of its highest values act as a margin to allow software to recognize and act upon timers that have expired before the time overflows the reach of the format. This period of a year (and a little bit more) should be enough to schedule an event (with a reasonable expiration) during the run-time of a program.
Hardware devices with 32.768 KHz quartz clocks are very common. This frequency is easily divided down to 128 Hz for a system clock. Since tic values represent relative time, they usually don't match the low-order half of the system absolute clock. 60 Hz is widely regarded as being just beyond the threshold of sensing visual change in an image by the human eye. Since 128 Hz is more than twice that, it should be adequate for scheduling computer events that happen faster than are observable. The trade-offs involved for the design of this time format system were studied over many years. I feel that it uses the best choices for a general purpose computer platform. Special purpose methods and systems can be designed for those rare applications that need them.
ϕ Character Type ch
Type ch is a 32-bit format that contains a single ϕText character. It is the unencoded form of text which is directly processed in software and is also referred to as the “ϕText Flat Character”. The low-order 21 bits (0∼20) record the character's Unicode Code Point. Bits 21∼23 contain its Style. This corresponds to a Type Face in publishing terminology. A character can have one of 8 Type Faces that can be used in any one document. Bits 24∼25 record the characters visual Size. Next is a 3-bit field (called Atb) that record individually settable attributes. Bit 26 (I) represents the characters Italic state. Bit 27 (U) is its Underscore state. Bit 28 (B) is its Bold state. Finally, the 3-bit field 29∼31 stores the character's Color Number. These field divisions are illustrated below:

Style codes are important for determining whether the text is Code or Comment. Only Style 0 is seen by the parser. Text with any other style is invisible to the parser. Style 0 should be configured for PhiBASIC font. This font has been specially designed to display characters as they should appear in all documents that contain ϕ source code. It must be a fixed pitch font with serifs. Sometimes documents contain pseudo-code that is only present as comments to describe what is going on. This is done using Style 1 which is a fixed pitch font with serifs. By default this is Courier New. Style 2 is used when documents contain descriptive text as you will see in the body of a book. By default this is configured to be Times New Roman. Style 3 is used for Headings and, has variable pitch and no serifs. By default this corresponds to Arial. The other Styles with codes 4∼7 are configurable using any fonts you wish. Text editing programs can only control the way text looks by using fonts. Many fonts do not contain glyphs for the characters that you need to see in your documents so this is done using Styles.
| Code | Style | Pitch | Serifs | Usage |
|---|---|---|---|---|
| 0 | PhiBASIC | Fix | Mild | Source Code |
| 1 | Courier New | Fix | Yes | Comments |
| 2 | Times New Roman | Var | Mild | Comments |
| 3 | Arial | Var | No | Comments |
| 4 | Undefined | Any | Any | Comments |
| 5 | Undefined | Any | Any | Comments |
| 6 | Undefined | Any | Any | Comments |
| 7 | Undefined | Any | Any | Comments |
Text documents are often subdivided into four levels of hierarchy. Use of different text sizes makes headings stand out. ϕText provides four text sizes which should be adequate for most documents. The smallest size is called Body and its code is 0. Most of the text in a document has this size. The lowest level of grouping is called Section and their headings have size 1. These are grouped into Chapters and their headings have size 2. They make the highest level of subdivision. Most documents have a Title at the very beginning of the document. Headings have size 3 which is the largest and least used size. The text sizes and their codes are tabulated below:
| Code | Name |
|---|---|
| 0 | Body |
| 1 | Section |
| 2 | Chapter |
| 3 | Title |
Three bits are provided in the ϕText flat character to let you individually set or clear the most common attributes in desk top publishing. These are Italic, Underscore and Bold. When the bit is clear, the attribute is turned off and the character looks normal. When set, it turns that attribute on. It probably makes no sense to italicize characters that are not alphabetic or text in non-European languages like Chinese. But you can still do it. ASCII, Unicode and most programming languages are Eurocentric and so is ϕText.
| Bit | Name |
|---|---|
| I | Italic |
| U | Underscore |
| B | Bold |
Color is another way of making text stand out. One kind of text that I like to use color for is labels. These are eliminated from some programming languages for one reason or another. Both C and ϕPPL use labels because typical control structures fall short of covering all the bases when it comes to conditionally executable code. I use suitable control structures where I can, but I still fall back on goto's in cases where control structures let me down. Labels are a particularly good place to use color. After seeing a reference to a label, you then may want to go searching for the place where the label is defined. If it begins with a red ♥ then it is much easier to find. If it has a larger size then it is even easier to find. The color codes were patterned somewhat after those in the rainbow or the well known resistor color code series. ϕText documents are supposed to assume a white background to simulate ink on white paper. So the lightest colors of white and yellow were excluded. Brown was substituted for yellow and Gray is provided in place of White. All color codes and their color assignments are tabulated below:
| Code | Color |
|---|---|
| 0 | Black |
| 1 | Red |
| 2 | Orange |
| 3 | Brown |
| 4 | Green |
| 5 | Blue |
| 6 | Purple |
| 7 | Gray |
ϕ's Error Status Type er
Type er is a 32-bit format that is often used to return the Status of a function call. This error coding system is used instead of exception handling like that in C++, C#, Java and Python. C and ϕPPL do not support frame stack unwinding because they are used to write operating system software. The try/throw/catch control structures in other programming languages are not supported. Stack unwinding is a very hazardous and computationally intense process to support in operating system code.
Encoding successes and other non-failures are just as important as encoding errors in returns from functions. They are so closely related that they are integrated into one system in ϕ. This system is supported in ϕAsm, ϕPPL and ϕOS. Functions often return a value of this data type and it can be easily tested by the caller to see if the call succeeded, failed or effectively did nothing. Any positive number is generally a success and the specific 31-bit number can be used by the function to qualify the kind of success. A return of 0 is generally used to indicate that no change has happened. I use it all the time in parsers to mean that what the routine was looking for was not found. If the value is negative then the high bit is set. The other 31 bits are divided into fields that identify ① the Realm where the error occured, ② what module defined the error and ③ what the specific error is. This information can be useful to the program in diagnosing what the problem was. The caller can either test for specific problems and try alternative actions or it can just report the number and exit.

When the value is negative then, bits 29 and 30 contain a 2-bit value reflecting the Realm in which the error occurred. The low-order 16 bits contains a number that identifies the compilation unit that defines the set of errors to which the specific error belongs. The Specific Error is a 13-bit number occupying bits 16 ∼ 28. This provides 8K different error codes for each compilation unit. A call can be made in ϕOS to produce as text string that describes the error.
ϕ's Flags Type flg
Flags are single bit memories that are packed into a byte and stored in either a hardware register or memory. A set of eight is called a Flag Set. Each flag within a set is given a single character name that is taken from the first character of its function. The Flag Set data type is shown below:
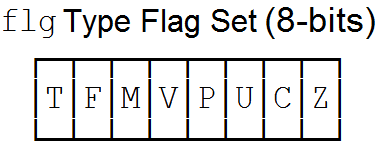
Z: Bit 0 is the Zero flag. It reflects whether the result of an operation is zero or not for both integers and floats.
C: Bit 1 is the Carry flag . For integer operations, it captures the carry out of the high-order bit. For float operations, it reflects that the result has overflowed and has been set to infinity.
U: Bit 2 is the Undefined flag. For integer operations it reflects that the result has been set to all 1's. For floating point operations, it reflects that the result has been set to NaN (interpreted as a NULL represented with ⊙ in ϕ).
P: Bit 3 is the Peg (integer) or Precision (float) flag. For integer operations it reflects whether the result has pegged out at a minimum or maximum signed integer value. The Minus bit can then be used to determine which of the two it is. For floating point operations, it reflects that there has been a loss of precision if set.
V: Bit 4 is the Overflow flag. For integers it reflects that the carry into the high-order bit is different from the carry out. For floating point operations it reflects that the result has been set to either Nan or Infinity. That is computed as (U | C).
M: Bit 5 is the Minus flag. It reflects that the result is negative. If an overflow occurs in an integer operation, the sign bit will usually be opposite of what it should be given a larger register to hold the result. This bit is set to the sign bit of the result in floating point operations.
F: Bit 6 is the Float flag. It records whether an operation is done as an integer instruction (F=0) or a floating point instruction (F=1). This is important because the same flags are shared between integer and floating point instructions. In some cases the flags are used differently and this flag is used to select the appropriate formula to interpret the other flags correctly.
T: Bit 7 is the Transfer flag. It is modified by the data transfer instructions and serves as an “End of File” indicator. It is also used in polling operations to indicate that a value is not yet ready to be read.
| Code | Symbol | Name |
|---|---|---|
| 0 | Z | Zero |
| 1 | C | Carry |
| 2 | U | Undefined |
| 2 | V | Overflow |
| 2 | M | Minus |
| 2 | F | Float |
| 7 | T | Transfer |
ϕ UTF-8 String Type stu
This type is a pointer to a UTF-8 encoded zero-terminated string. Literals are expressed using the ASCII double quotes for example "The dog barks.". In the post-Unicode world, C libraries are updated to handle UTF-8 byte streams instead of ASCII strings. When the contents of strings are all ASCII then the product is the same. Note that pointers into their sequences can not be interpreted as characters.
ϕTSE String Type stg
Type stg is a pointer to a zero-terminated string with ϕTSE encoded bytes. String Literals are placed between left and right double quotes example “The cat's Meow.”.
ϕName String Type stn
Type stn is
a pointer to a zero-terminated string of ϕName encoded bytes.
Constant strings often point into the executable while
variable strings usually point into the local heap.